A TS approach for clustering time dependent data

I dati

I dati sono una collezione di attività di allenamento registrati con degli sport-watch di atleti di varie discipline (corsa, nuoto, ciclismo, …).

La motivazione iniziale della raccolta era quella di lavorare con dati di una realtà emergente che mi coinvolgeva in prima persona

• Periodi di raccolta: dal 10/2017 al 12/2017 e dal 10/2020 al 12/2020
• Luogo di raccolta: Strava, gruppi Facebook, conoscenze, …
• Tipo di dato: file .json, .tcx, .gpx, .fit, .csv, …
• Numero di atleti ad oggi: 23
• Numero di attività totali: 4315
• num. min. di attività per soggetto: 1
• num. max. di attività per soggetto: 1430
• Altri dataset disponibili su: Kaggle, trackeR (Frick and Kosmidis, 2017),…

Ciascun file contiene dati raccolti nel tempo e nello spazio di una o più variabili di interesse, tra le quali:

• Data ed ora
• Posizione GPS
• Altitudine
• Battito cardiaco (Heart Rate)
• Velocità (speed & vertical speed)
• Cadenza (passi al minuto)
• Potenza (di pedalata, per i ciclisti)
• …

Gli orologi più recenti sono in grado di misurare l’ossigenazione del sangue, il lattato, la concentrazione di glucosio, il che li fa diventare un oggetto importante per il monitoraggio costante della salute.

Il pacchetto trackeR contiene una serie di routine utili per l’analisi retrospettiva di questa tipologia di dati.

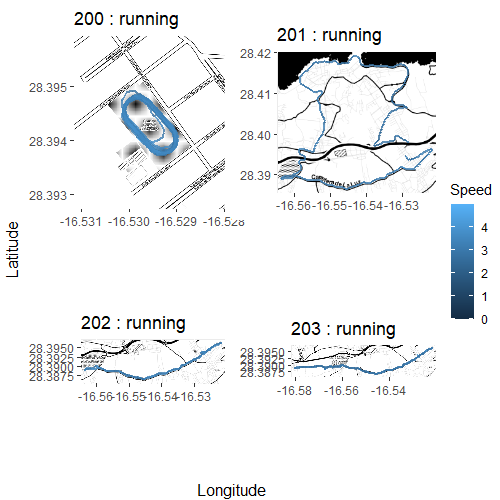
I dati come funzioni nello spazio

I dati come serie storiche

I dati mostrano dinamiche complesse dovute alla struttura dell’allenamento (nota all’atleta)

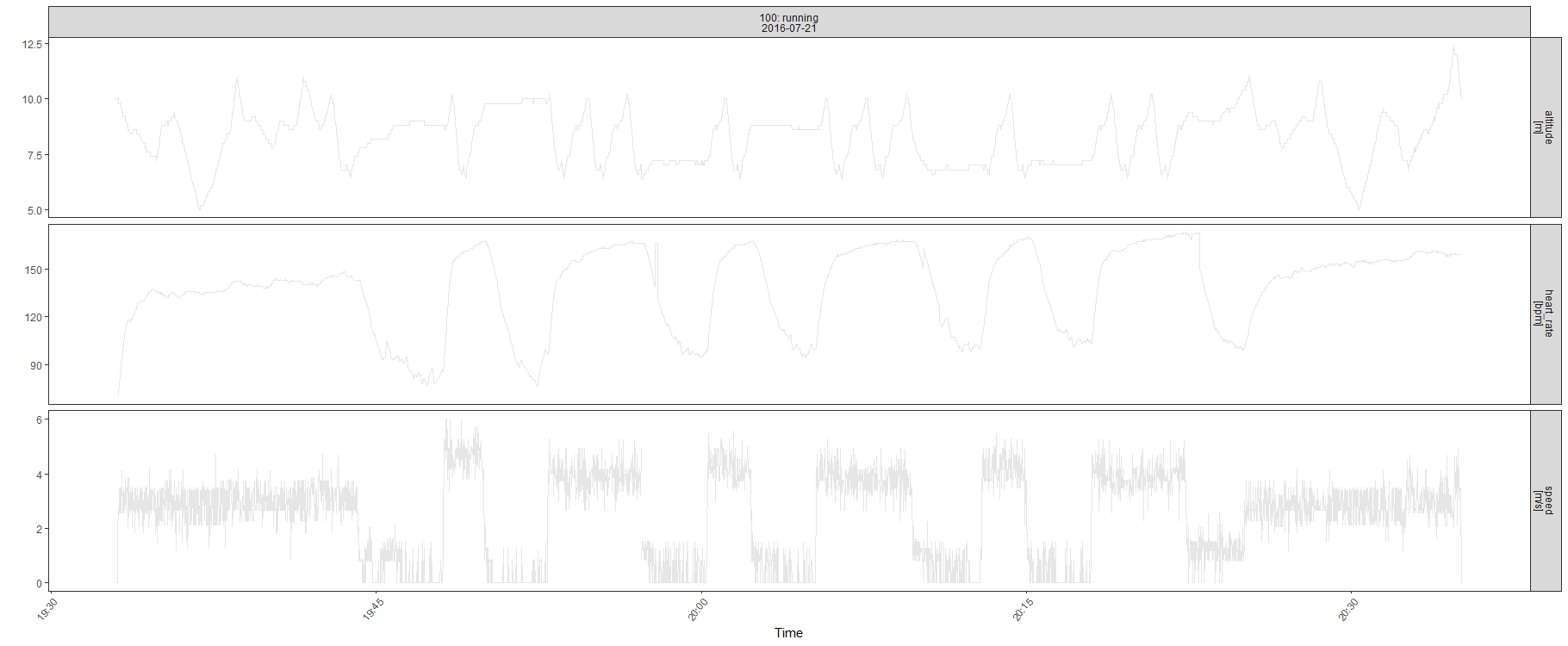
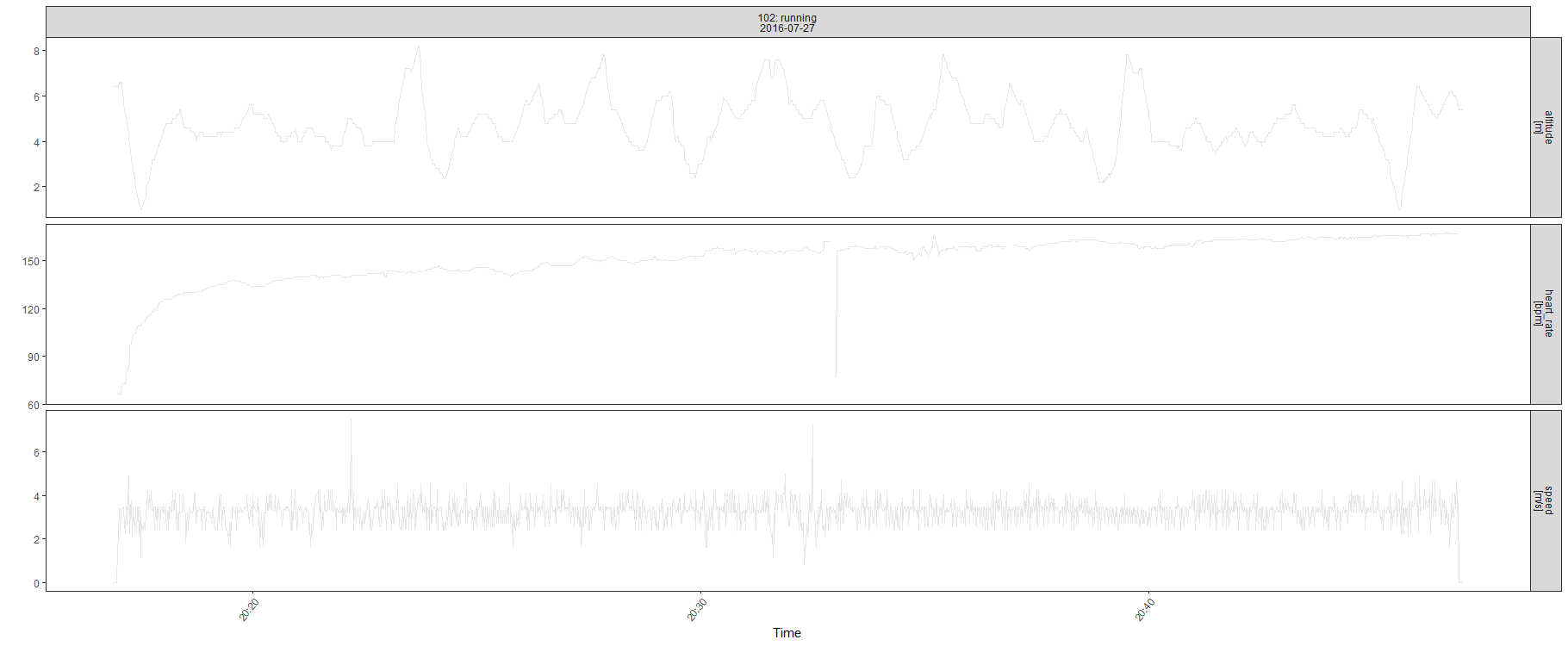
Alle volte le attività presentano un comportamento più regolare, ma comunque possono essere affette dalla presenza di dati mancanti e osservazioni anomale.

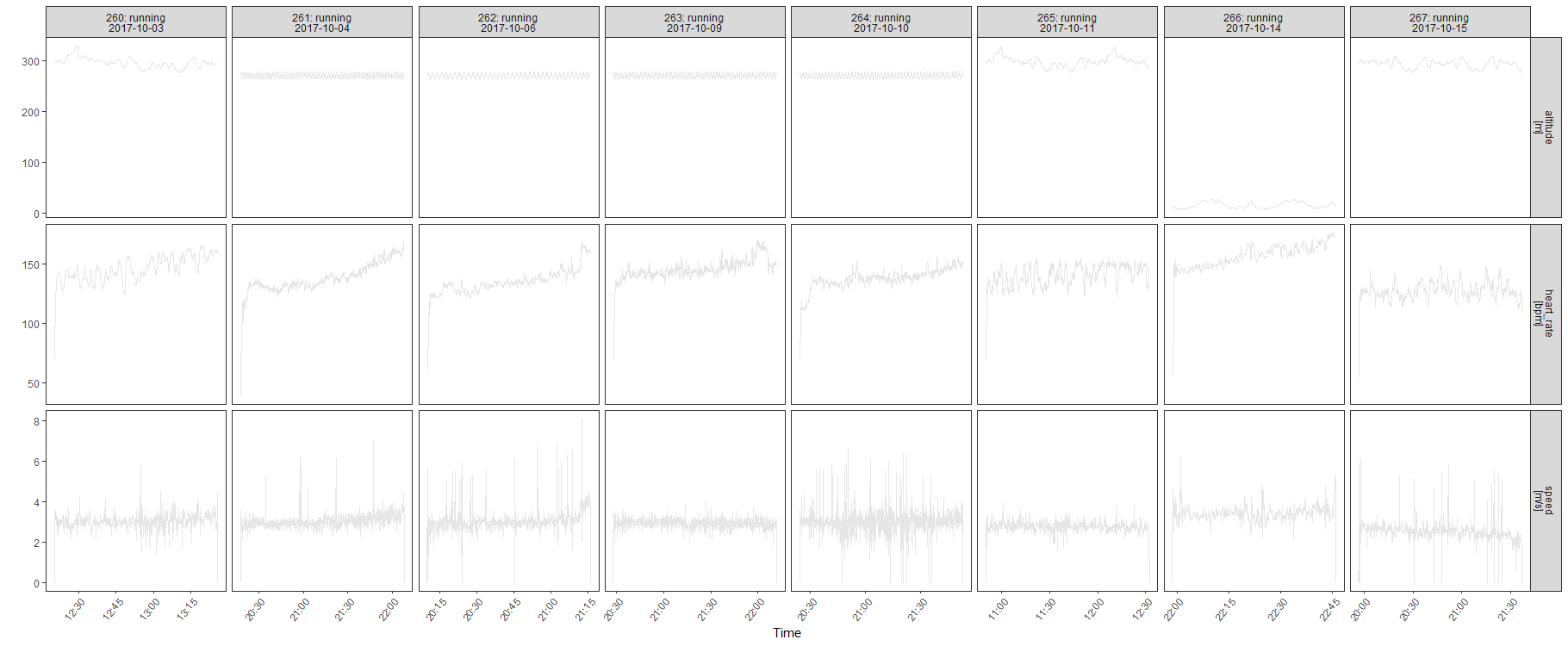
I dati come serie storiche di serie storiche

Cosa fare?

Quindi cosa possiamo fare in questo mare di dati complessi?

“Disperarsi, naturalmente!” cit. il tricheco in 136

Perché state space

I modelli state space sono utili perché:

1. permettono di gestire automaticamente dati mancanti
2. offrono versatilità nella costruzione di modelli, in quanto permettono di gestire all’interno di uno stesso framework trend, comportamenti periodici, l’inclusione di covariate, etc.
3. permettono di gestire online flussi di dati

Riteniamo particolarmente rilevante il punto 3, perché in questo contesto è utile avere feedback affidabili mentre l’attività viene svolta (potrebbe essere utile anche per motivi di salute).

Perché il clustering

“Identifying activities that require similar effort allows to know how one athlete is performing. A different response to the same stimuli might be due to the enhancement or worsening of physical conditions, as well as to the impaired health of the athlete.” cit. Un vecchio saggio

Il modello

• Sia \(y_{p,n,t}\) lo scalare che denota la \(p\)-esima variabile, per l’attività \(n\)-esima, al tempo \(t\), per \(p = 1,\ldots, P\), \(n = 1, \ldots, N\), e \(t = 1,\ldots, T\).

• Assumiamo che le \(N\) attività possono essere raggruppate in \(G\) gruppi diversi.

• Immaginiamo di sapere che la \(n\)-esima attività appartenga al gruppo \(g\); allora la sua osservazione nel tempo segue un modello dinamico lineare tale che \(y_{p,n,t} = \mu_{p,t}^{(g)} + \upsilon_{p, n, t} = \sum _{g=1}^G \mathbb{I}(S_n = g) \mu_{p,t}^{(g)} + \upsilon_{p, n, t},\) per \(t = 1, \ldots, T\), \(p = 1,\ldots, P\), qualche specificazione del trend \(\mu_{p,t}^{(g)}\) ed errori incorrelati.

• \(\boldsymbol{\mu}_t^{(g)} = \begin{bmatrix}\mu_{1,t}^{(g)}& \mu_{2,t}^{(g)}& \ldots& \mu_{P, t}^{(g)}\end{bmatrix}^\intercal\) contiene i trend al tempo \(t\) condivisi dalle attività appartenenti al gruppo \(g\), per le \(P\) variabili osservate.

• L’appartenenza al gruppo \(g\) per l’attività \(n\) non cambia nel tempo.

• Attività appartenti allo stesso gruppo condividono le intere traiettorie descritte dai trend \(\mathbf{M}_{1:T}^{(g)}=\begin{bmatrix}\boldsymbol{\mu}_1^{(g)}& \boldsymbol{\mu}_2^{(g)}&\ldots& \boldsymbol{\mu}_T^{(g)}\end{bmatrix}\).

• I trend della stessa variabile e diversi gruppi seguono le stesse relazioni strutturali, mentre variabili diverse possono seguire relazioni strutturali diverse.

Un esempio

Immaginiamo di osservare \(P = 2\) variabili per \(N\) attività. Un semplice modello per \(G\) gruppi può essere descritto dal seguente modello

\[\texttt{Prima variabile}\quad\begin{cases} y_{1,n,t} &= \sum_{g=1}^G\mathbb{I}(S_n = g) \mu_{1,t}^{(g)} + \upsilon_{1,n,t}\\ \mu_{1,t+1}^{(g)} &= \mu_{1,t}^{(g)}+ \epsilon_{1,t}^{(g)}, \end{cases}\] \[\texttt{Seconda variabile}\quad\begin{cases} y_{2,n,t} & = \sum_{g=1}^G \mathbb{I}(S_n = g) \mu_{2,t}^{(g)} + \upsilon_{2,n,t}\\ \mu_{2,t+1}^{(g)} & = \mu_{2,t}^{(g)}+ \beta_{2,t}^{(g)}+ \epsilon_{2,t}^{(g)}\\ \beta_{2, t+1}^{(g)} & = \beta_{2, t}^{(g)} + \eta_{2,t}^{(g)}, \end{cases}\]

per una qualche specificazione di \(\mu_{1,1}^{(g)}\), \(\mu_{2,1}^{(g)}\), \(\beta_{2,1}^{(g)}\), \(g = 1, \ldots, G\), \(t=1,\ldots, T\) e \(n=1,\ldots, N\).

Forme matriciale e vettorizzata del modello

Dopo un po’ di trick algebrici possiamo ottenere sia una forma matriciale del modello

\[\mathbf{Y}_t = \mathbf{Z} \mathbf{A}_t \mathbf{S}^\intercal + \mathbf{\Upsilon}_t, \quad \mathbf{\Upsilon}_t \sim \text{MN}_{P,N}(\mathbf{0}, \mathbf{\Sigma}^R \otimes \mathbf{\Sigma}^C ), \\ \mathbf{A}_{t+1} = \mathbf{T} \mathbf{A}_t + \mathbf{\Xi}_t, \quad \mathbf{\Xi}_t \sim \text{MN}_{Q,G}(\mathbf{0}, \mathbf{\Psi}^R \otimes\mathbf{\Psi}^C ),\]

per qualche valore di partenza \(\mathbf{A}_1\), sia una forma vettorizzata

\[\mathbf{y}_t = (\mathbf{S} \otimes \mathbf{Z}) \boldsymbol{\alpha}_t + \boldsymbol{\upsilon}_t, \quad \boldsymbol{\upsilon}_t \sim \text{MVN}_{PN}(\mathbf{0}, \mathbf{\Sigma}^C \otimes \mathbf{\Sigma}^R ), \\ \boldsymbol{\alpha}_{t+1} = (\mathbf{I}_G \otimes \mathbf{T})\boldsymbol{\alpha}_{t} + \boldsymbol{\xi}_{t}, \quad \boldsymbol{\xi}_t \sim \text{MVN}_{QG}(\mathbf{0}, \mathbf{\Psi}^C \otimes \mathbf{\Psi}^R ),\]

con \(\mathbf{y}_t =\text{vec}(\mathbf{Y}_t)\), \(\boldsymbol{\alpha}_{t} = \text{vec}(\mathbf{A}_t)\), \(\boldsymbol{\upsilon}_{t} = \text{vec}(\mathbf{\Upsilon}_t)\) e \(\boldsymbol{\xi}_{t} = \text{vec}(\mathbf{\Xi}_t)\).

Una generalizzazione del modello prevede di considerare per l’equazione di misura una somma di fattori latenti \(\sum_{r=1}^{R} \mathbf{Z}_r \mathbf{A}_{r,t} \mathbf{S}_r^\intercal\) anziché solo \(\mathbf{Z} \mathbf{A}_{t} \mathbf{S}^\intercal\), così da poter includere anche elementi che possono essere considerati di disturbo (errori correlati, effetti di regressione,…).

Esempio

Sia \(\mathbf{Y}_t= \begin{bmatrix}\mathbf{y}_{t}^{\cdot 1} & \ldots &\mathbf{y}_{t}^{\cdot N} \end{bmatrix}\) con

\[\mathbf{y}_{t}^{\cdot n} = \begin{bmatrix} \texttt{HeartRate(bpm)}_{n,t}\\ \texttt{Speed(m/s)}_{n,t}\\ \texttt{Cadence(spm)}_{n,t}\\ \end{bmatrix}\]

e \(\mathbf{X}_t = \text{diag}(x_{1,t}, x_{2,t}, \ldots, x_{N,t})\), con

\[x_{n,t} = \texttt{Altitude(m)}_{n,t}-\texttt{Altitude(m)}_{n,t-1}.\]

Consideriamo il modello

\[\mathbf{Y}_t = \mathbf{B} \mathbf{S}^\intercal \mathbf{X}_t + \mathbf{Z} \mathbf{A}_t \mathbf{S}^\intercal + \mathbf{\Upsilon}_t, \quad \mathbf{\Upsilon}_t \sim \text{MN}_{P, N}(\mathbf{0}, \mathbf{\Sigma}^R \otimes \mathbf{\Sigma}^C),\\ \mathbf{A}_{t+1} = \mathbf{T}\mathbf{A}_t + \mathbf{\Xi}_t, \quad \mathbf{\Xi}_t \sim \text{MN}_{Q,G}(\mathbf{0}, \mathbf{\Psi}^R \otimes \mathbf{\Psi}^C),\]

con \(\mathbf{A}_{1} \sim \text{MN}_{Q,G}(\hat{\mathbf{A}}_{1 \mid 0}, \mathbf{P}_{1 \mid 0}^R \otimes \mathbf{P}_{1 \mid 0}^C)\) e \(\mathbf{B} \sim \text{MN}_{P,G}(\hat{\mathbf{B}}_{0}, \mathbf{P}_{B}^R \otimes \mathbf{P}_{B}^C).\)

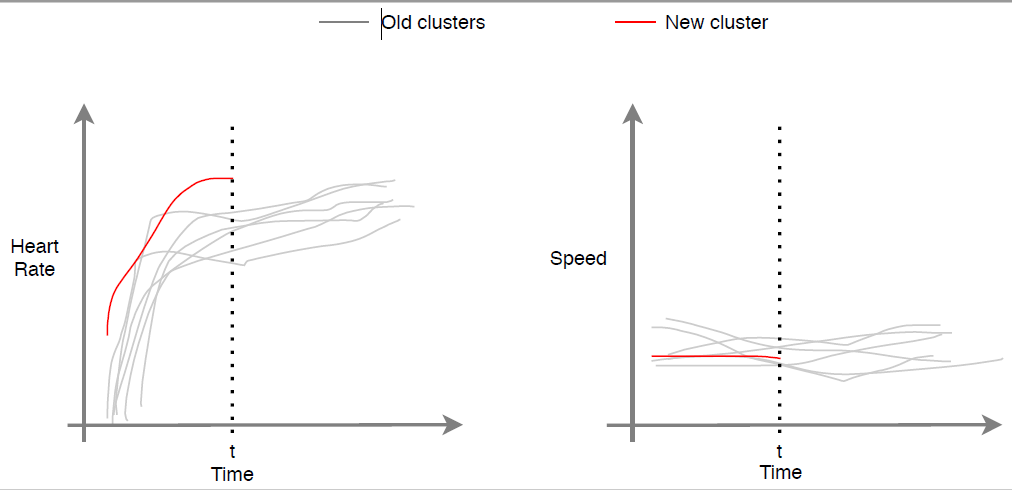
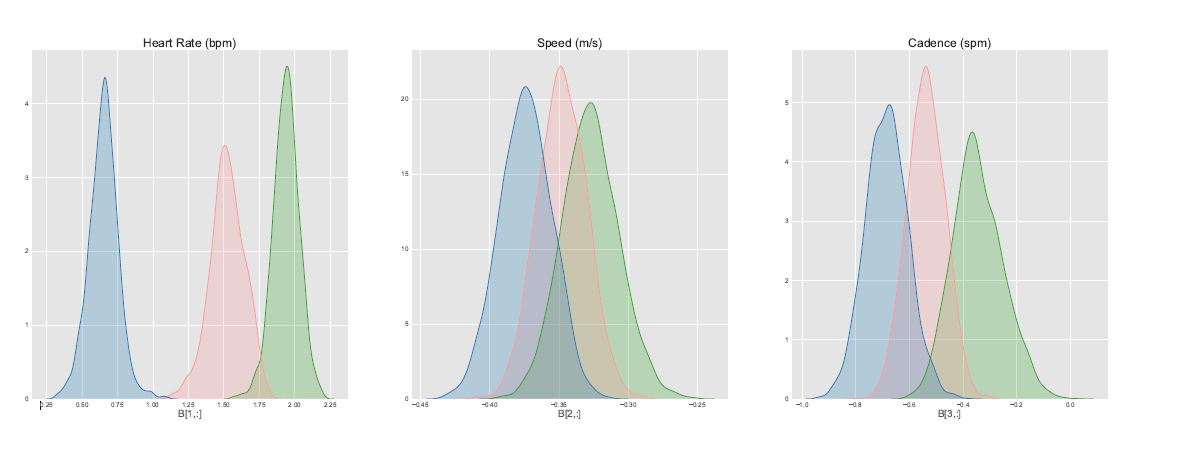
• Il modello identifica gruppi di attività che richiedono sforzi simili, dopo aver controllato per variazioni di altitudine, che possono avere un effetto sulla risposta.

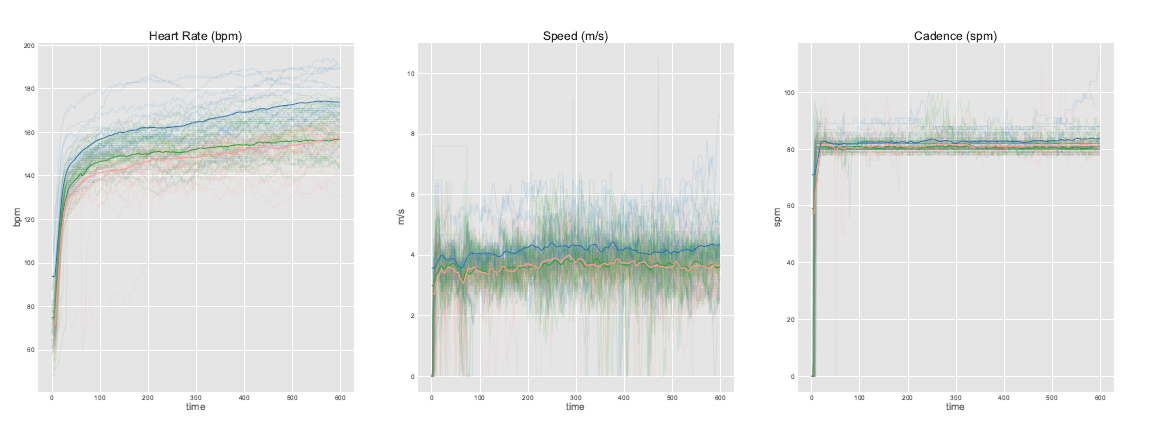
• Coi dati reali utilizzeremo \(P = 3\), \(N = 90\), \(G = 3\), \(Q = 4\) (HR: LLT model, Speed: LLM, cadence: LLM), e \(T = 600\) secondi.

Risultati

Take home message

• Un approccio state space consente di costruire ad hoc modelli con dinamiche complesse o di cui si ha conoscenza a priori (periodicità, cambi deterministici del livello, …)
• Offre un framework unificato per ottenere quantità utili all’inferenza, anche con la presenza di dati mancanti
• Permette il monitoraggio delle serie storiche online e la possibilità di fare previsioni in avanti
• Potrebbe richiedere una serie di accorgimenti computazionalmente dispendiosi nel caso di dati funzionali
• I miei dati non sono matriciali in partenza, ma la loro rappresentazione matriciale permette di includere forme di dipendenza in modo parsimonioso

E per chi volesse giocare con questi dati: correte e giocate con (trackeR)