Ladies and gentlemen… On your marks!

Mixture models

Si consideri la seguente specificazione gerarchica di un modello mistura

\[Y_{n} \mid S_{n}=g, \theta_{g} \sim f\left(\cdot \mid \theta_{g} \right), \quad n =1,\ldots, N\] \[S_{n} \mid \pi_G \sim \text{Mult}_G\left(1, \pi_G \right), \quad \pi_G \sim \text{Dir}_G(\pi_0),\] \[\theta_g \sim p(\cdot \mid \theta_{0,g}), \quad g=1,\ldots,G,\] \[G \sim p(\cdot \mid G_0),\]

per il quale è di interesse svolgere una qualche analisi a posteriori, una volta osservato un campione \(N\) dimensionale \(y_{1:N}\)

MCMC & Cluster Allocations

Un approccio elementare al problema prevede l’utilizzo di algoritmi MCMC (Gibbs Sampler, MH within Gibbs, …).

Generalmente, questi algoritmi simulano iterativamente dalle full conditional dei parametri

Le allocazioni vengono aggiornate una alla volta condizionatamente al resto

\[S_n \mid S_{1:(n-1), (n+1):N}, \theta_{1:G},\pi, {y}_{1:N}\]

in accordo con la loro distribuzione full conditional

Con \(N\) grande, calcolare le distribuzioni full conditional può essere oneroso e portare a catene mal mixate

Inoltre…

… abbiamo altri problemi!

L’esplorazione di tutte le mode non è garantita

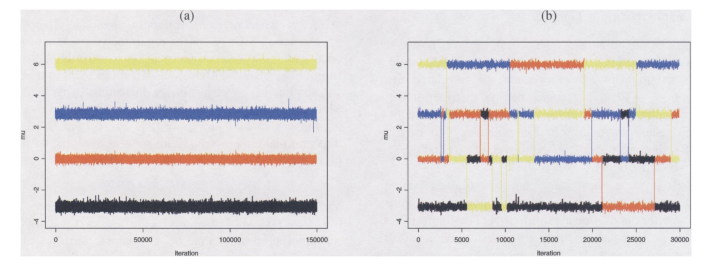
In high-dimensional settings la catena si incastra e non cambia le allocazioni

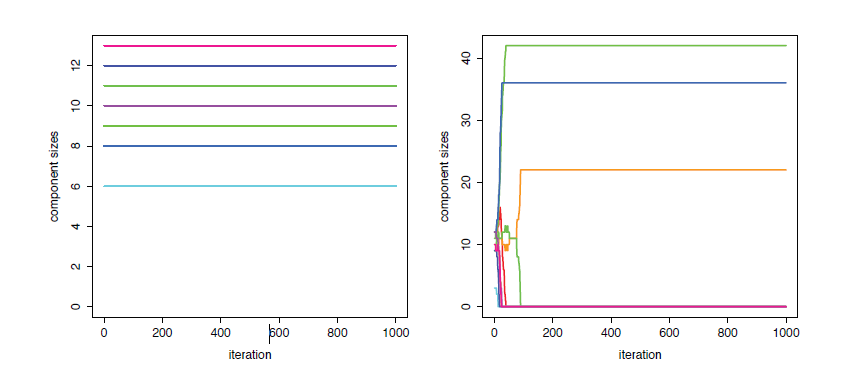
Risolviamoli: meglio insieme!

Possiamo considerare le allocazioni

\[S_{1:N} = (S_1, S_2, \ldots, S_N) \in \{1, 2, \ldots, G\}^N\]

come un unico parametro o, alternativamente, la matrice di selezione

\[\mathbf{S} = \begin{bmatrix}\mathbb{I}(S_1 =1) & \mathbb{I}(S_1 =2) & \cdots & \mathbb{I}(S_1 =G)\\ \mathbb{I}(S_2 =1) & \mathbb{I}(S_2 =2) & \cdots & \mathbb{I}(S_2 =G)\\ \vdots & \vdots & \vdots & \vdots \\ \mathbb{I}(S_N =1) & \mathbb{I}(S_N =2) & \cdots & \mathbb{I}(S_N =G) \end{bmatrix} \in \mathcal{S}^{N,G}\]

e considerare in one-step le loro distribuzioni full conditional (eventualmente marginalizzando una parte di parametri)

Qualche riferimento

• Nobile and Fearnside (2007) Bayesian finite mixtures with an unknown number of components: the allocation sampler (Stat Comput)

• Fong, Wakefield and Rice (2012) An efficient Markov chain Monte Carlo method for mixture models by neighborhood pruning (JCGS)

• Schäfer and Chopin (2013) Sequential Monte Carlo on Large Binary Sampling Spaces (Stat Comput)

• Titsias and Yau (2017) The Hamming ball sampler (JASA)

• Zanella (2020) Informed proposals for local MCMC in discrete spaces (JASA)

The allocation sampler

L’algoritmo considera le allocazioni e il numero di gruppi congiuntamente, dopo aver integrato via i parametri del modello (quando possibile)

È composto da due tipi di moves (stocastiche):

• Quelle che non cambiano il numero di gruppi \(G\)
• Quelle che cambiano il numero di gruppi

Pro

• Rimane lo stesso indipendentemente dal numero di osservazioni o dalla famiglie che compongono la mistura
• Non richiede l’invenzione di buone jumping moves tipiche delle tecniche di reversible jump

Cons (opinione basata su prove empiriche)

• Quando la dimensione di una singola osservazione \(y_n\) tende a crescere diventa difficile fare tuning

Fixed G: M1 & M3

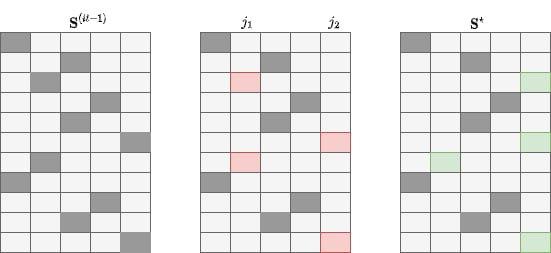
1. Seleziona casualmente \(j_1\) e \(j_2\)
2. Rialloca gli elementi nei gruppi \(j_1\) e \(j_2\) in \(j_1\) con probabilità \(p\) e in \(j_2\) con probabilità \(1-p\)

Nelle due moves cambia come si sceglie \(p\) (M1: \(p \sim \beta(a, a)\), M3: basata sulla likelihood)

Fixed G: M2 & M4

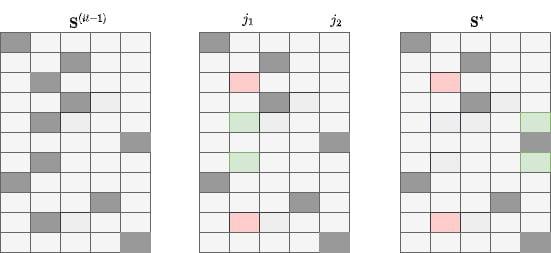
1. Seleziona casualmente \(j_1\) e \(j_2\)
2. Seleziona casualmente \(m \in \{1,\ldots, n_{j1}\}\)
3. Selezione casualmente \(m\) elementi di \(j_1\) e allocali in \(j_2\)

Tra le moves che non cambiano il numero di gruppi viene considerata anche quella dove vengono casualmente cambiate le label dei gruppi

Varying G (caso \(G^\star = G^{(it-1)}+1\))

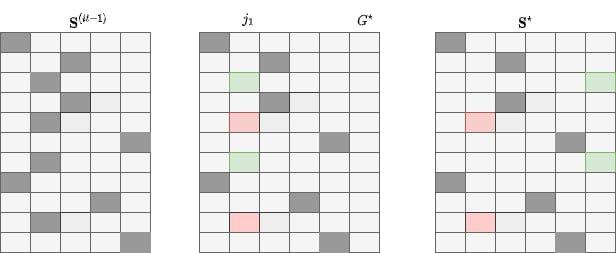
1. Seleziona casualmente \(j_1 \in \{1, \ldots, G^{(it-1)}\}\)
2. Alloca gli elementi di \(j_1\) in \(j_2 = G^\star\) con probabilità \(p_e \sim \beta(a, a)\)

$a$ è un parametro critico per il buon funzionamento dell’algoritmo

Una nuova move (fixed G)

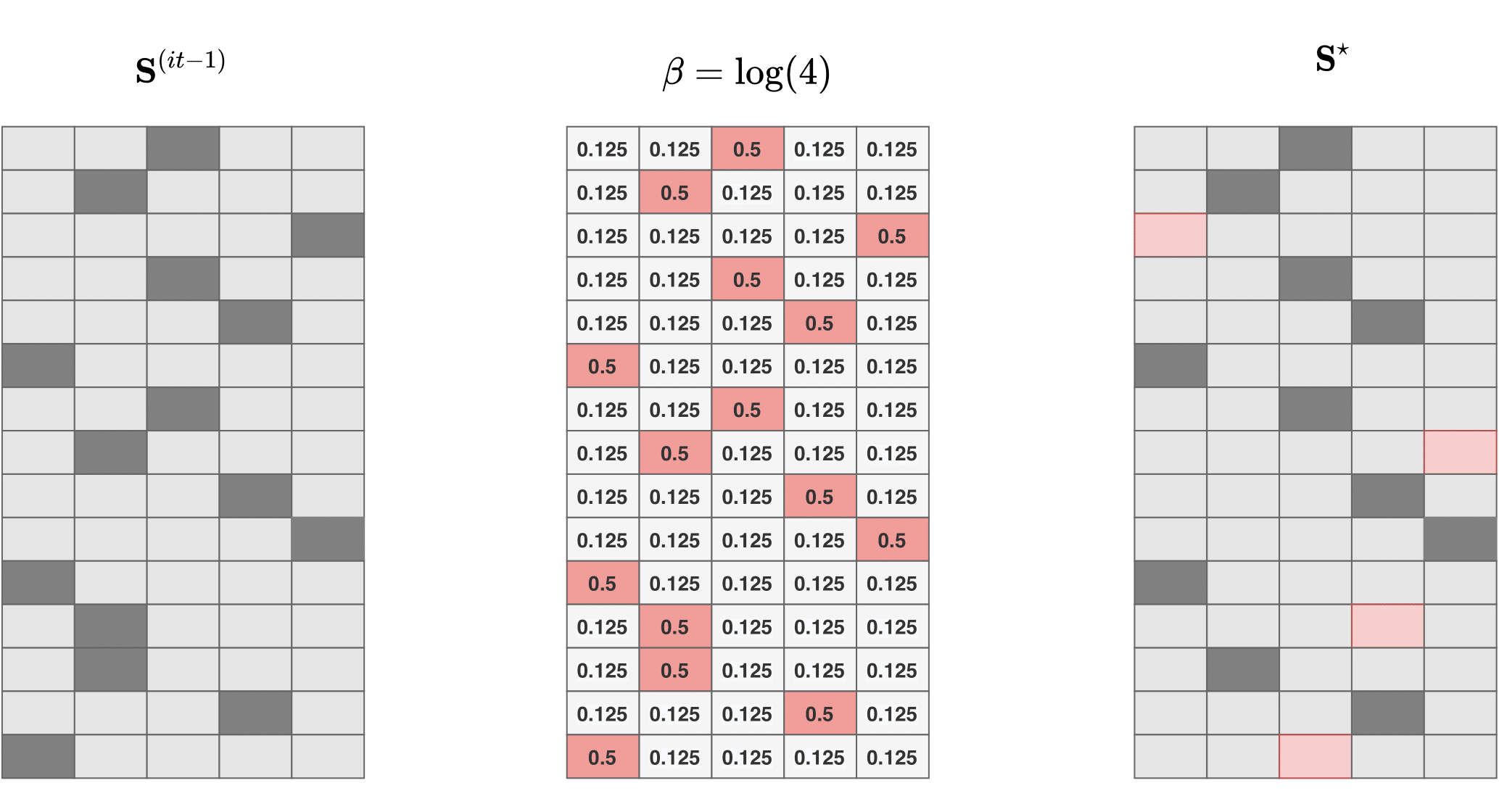
Dato \(\mathbf{S}^{(it-1)}\), ogni riga di \(\mathbf{S}^\star\) viene generata indipendentemente dalle altre in accordo con

\[\operatorname{Pr}\left(S_{n}^{\star}=j \mid S_{n}^{(it-1)}\right)=\frac{\exp \left(\beta \mathbb{I}\left(S_{n}^{(it-1)}=j\right)\right)}{\sum_{g=1}^{G} \exp \left(\beta \mathbb{I}\left(S_{n}^{(it-1)}=g\right)\right)}\]

The Hamming ball sampler

Algoritmo MCMC per l’inferenza in modelli che involvono high-dimensional discrete state spaces

Viene introdotta una variabile ausiliaria \(\mathbf{U}\) per la costruzione di uno spazio di esplorazione che viene troncato adattivamente

La particolare costruzione permette la derivazione di un Gibbs sampler

Richiede la definizione di una palla centrata in \(\mathbf{S}\) e di raggio \(m\) (la Hamming ball di raggio \(m\)), per cui \(m\) può essere inteso come un parametro di tuning che può influenzare velocità ed efficacia dell’algoritmo

Costruzione

Viene considerata la seguente fattorizzazione della distribuzione congiunta (aumentata)

\[p(y_{1:N}, \theta, \mathbf{S}, \mathbf{U}) = p(\mathbf{y}_{1:N}, \theta, \mathbf{S}) p(\mathbf{U} \mid \mathbf{S})\]

dove

\[p(\mathbf{U} \mid \mathbf{S}) = \dfrac{1}{Z_m} \mathbb{I}(\mathbf{U} \in \mathcal{H}_m(\mathbf{S}))\]

è una distribuzione uniforme su $\mathcal{H}_m(\mathbf{S})$,

\[\mathcal{H}_m(\mathbf{X}) = \left\lbrace\mathbf{U}\colon d\left(\mathbf{u}_n, \mathbf{x}_n\right) \leq m,\; n=1,\dots,N\right\rbrace\]

è la Hamming ball di raggio \(m\) e \(d\left(\mathbf{u}_n, \mathbf{s}_n\right)\) è la distanza di Hamming tra i blocchi \(\mathbf{u}_n\) e \(\mathbf{s}_n\) di \(\mathbf{U}\) e \(\mathbf{S}\), rispettivamente

Gibbs sampler

Data la particolare costruzione dello state space, l’algoritmo itera i seguenti passi

1. \[\mathbf{U} \leftarrow p(\mathbf{U} \mid \mathbf{S})\]
2. \[\mathbf{S} \leftarrow p( \mathbf{S} \mid \theta, \mathbf{U}, y_{1:N})\]
3. \[\theta \leftarrow p(\theta \mid \mathbf{S}, y_{1:N})\]

dove gli step 2 e 3 possono essere accorpati se disponibile un buon passo Metropolis

Il ruolo di \(\mathbf{U}\) è quello di fare decluttering, localizzando la ricerca di \(\mathbf{S}\)

A differenza di un classico passo Metropolis, le proposte di \(\mathbf{S}\) vengono sempre accettate

Informed proposals

Zanella (2020) propone un framework per la costruzione di proposal informate in spazi discreti di dimensione notevoli

Usando un confronto Peskun-type tra kernel, caratterizza esplicitamente la classe delle locally balanced proposals, cioè le proposal ottime in questo framework

Gli algoritmi che ne risultano sono semplici da implementare e più efficienti se comparati alle attuali proposte, comprese le versioni HMC discrete

(Personalmente è un paper che ho trovato difficile, per cui non saprei spiegarlo in due slide o parole, anche se promettente e utile per il mio modello e molti altri contesti)

Take home message

• Gli algoritmi proposti generalmente lavorano localmente

• Volendo costruire un algoritmo per simulare in spazi discreti è necessario che la ricerca dei vicini (e il calcolo di eventuali quantità utili all’algoritmo) sia fattibile

• Esistono varie rappresentazioni matematiche di uno stesso concetto, che possono influenzare i risultati e aprire nuove strade sia da un punto di vista modellistico che algoritmico (labels, matrici di selezione, partizione di $N$ elementi)

Le vostre proposte

Articoli correlati

• Jain and Neal (2004) A Split-Merge Markov Chain Monte Carlo Procedure for the Dirichlet Process Mixture Model (JCGS)

• Ni, Müler, Diesendruck, Williamson, Zhu and Ji (2020) Scalable Bayesian Nonparametric Clustering and Classification (JCGS)