Generalized Variational Inference and its properties

Struttura del paper

L’articolo dal titolo “Generalized Variational Inference: Three arguments for deriving new Posteriors” di Jeremias Knoblauch, Jack Jewson e Theodoros Damoulas disponibile su arXiv è strutturato nei seguenti punti:

1. Presentazione di un paradigma unificato per l’inferenza Bayesiana
2. Risultato di ottimalità sulla “standard” Variational Inference (VI)
3. Generalized Variational Inference (GVI) e le sue proprietà
4. Algoritmo Black-Box per l’inferenza
5. Applicazioni alle Bayesian Neural Networks e a Processi Gaussiani

…e una lunga appendice tecnica!

In questo breve post mi occuperò di presentare gli argomenti in grassetto.

Assunzioni nell’inferenza Bayesiana

Lo scopo dell’inferenza Bayesiana è quello di trovare una distribuzione a posteriori per i parametri \(q^*_B(\mathbf{\vartheta})\), data una prior \(\pi(\mathbf{\vartheta})\) e un modello per i dati osservati. Assunzioni di base sono:

1. P: Corretta specificazione della Prior, nel senso che debba rappresentare la miglior conoscenza che abbiamo
2. L: Esiste un parametro per il quale la Likelihood coincide esattamente con il processo generatore dei dati
3. C: I tempi e la potenza Computazionale sono infiniti

Se questi tre punti valgono, allora la posteriori \(q^*_B(\mathbf{\vartheta})\) è l’unica distribuzione desiderabile!

Ma nella pratica…

1. P: La complessità e l’ammontare di parametri rende impossibile specificare correttamente la conoscenza a priori!
2. L: Tutti i modelli sono sbagliati!
3. C: I tempi e la potenza computazionale limitata per modelli molto complessi!

La regola del 3

Un primo contributo degli autori consiste nel giustificare la scrittura di un qualsiasi problema Bayesian in un modo molto generale \(P(\ell_n,\mathcal{D},\Pi)\):

\[q_B^*(\mathbf{\vartheta}) = \arg\min_{q\in\Pi}\,\mathcal{L}(q\mid\mathbf{x},\ell_n,\mathcal{D}),\]

e in particolare:

\[\mathcal{L}(q\mid\mathbf{x},\ell_n,\mathcal{D})=\mathbb{E}_{q(\mathbf{\vartheta})}\left[\ell_n(\mathbf{\vartheta},\mathbf{x})\right] + \mathcal{D}(q\mid\pi),\]

similmente all’approccio di Bissiri et al, 2016.

Il nome regola del 3 deriva dal fatto che per questo paradigma è necessario specificare solo 3 quantità fondamentali:

1. Loss \(\ell_n\): collega i parametri alle osservazioni. 2. Uncertainty quantifier \(\mathcal{D}\): solitamente una divergenza. Ha la funzione di determinare l’incertezza nella posteriori. 3. Admissible posteriors \(\Pi \subseteq \mathcal{P}(\Theta)\): un insime di possibili distribuzioni valide tra cui cercare la posteriori.

Un caso particolare si ha quando \(\Pi\) è una famiglia di distribuzioni variazionali \(\mathcal{Q}\) e l’inferenza che si ottiene è detta Variational Bayes.

“Standard” Variational Inference (VI)

Con la dicitura “standard” ci riferiamo al caso in cui la loss function sia la negative log-likelihood e la divergenza scelta sia la Kullback-Leibler \(P(-\log p(\mathbf{x}\mid\mathbf{\vartheta}),\mathsf{KL},\mathcal{Q})\). Solitamente si forniscono due principali interpretazioni:

1. VI come massimizzazione dell’evidenza (ELBO)
2. VI come minimizzazione della divergenza

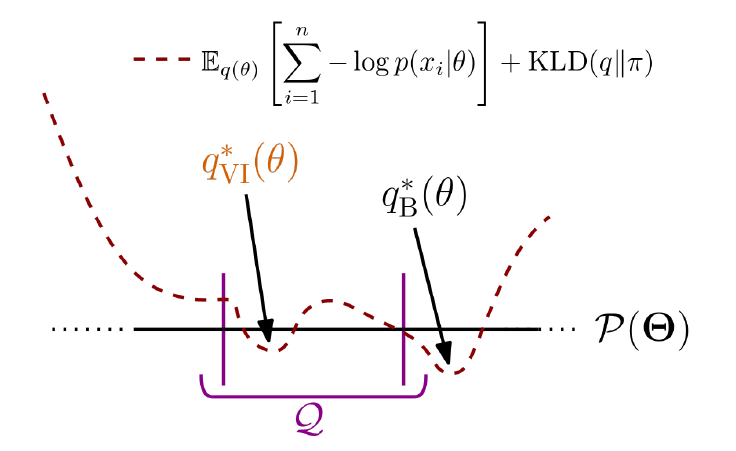
Grazie alla scrittura del problema Bayesiano mediante la regola del 3, gli autori suggeriscono di interpretare VI come un problema di ottimizzazione vincolato.

Un risultato teorico interessante dice che la VI standard garantisce la posterior ottimale all’interno di \(\mathcal{Q}\) e ogni altro metodo alternativo (ad esempio divergenze diverse dalla Kullback-Leibler) è sub-ottimale.

Questo però non è sempre vero nella pratica! Allora gli autori propongono il framework più generale possibile, chiamato Generalized Variational Inference.

Generalized Variational Inference

GVI porta a delle posteriori che hanno delle proprietà molto interessanti rispetto alle assunzioni di base dell’inferenza Bayesiana. In particolare:

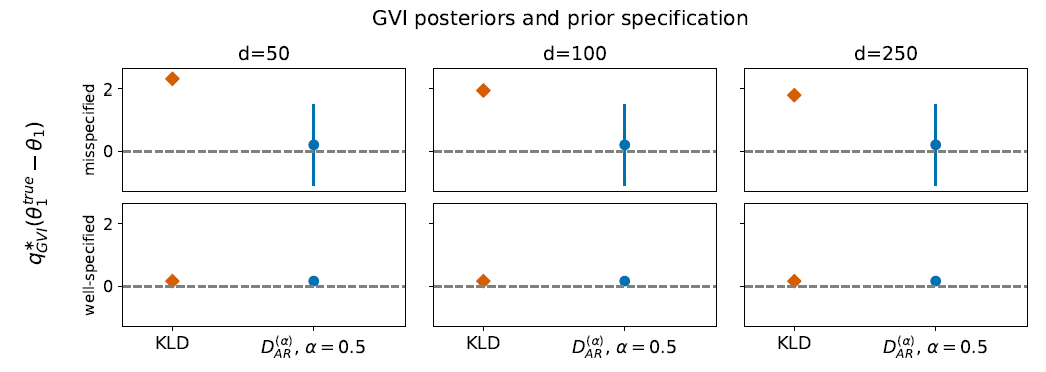
1. P: è robusta rispetto misspecificazioni della prior
2. L: è robusta rispetto a errata specificazione del modello per i dati
3. C: riduce sensibilmente i costi computazionali (questo punto vale in genere per tutta l’inferenza variazionale)

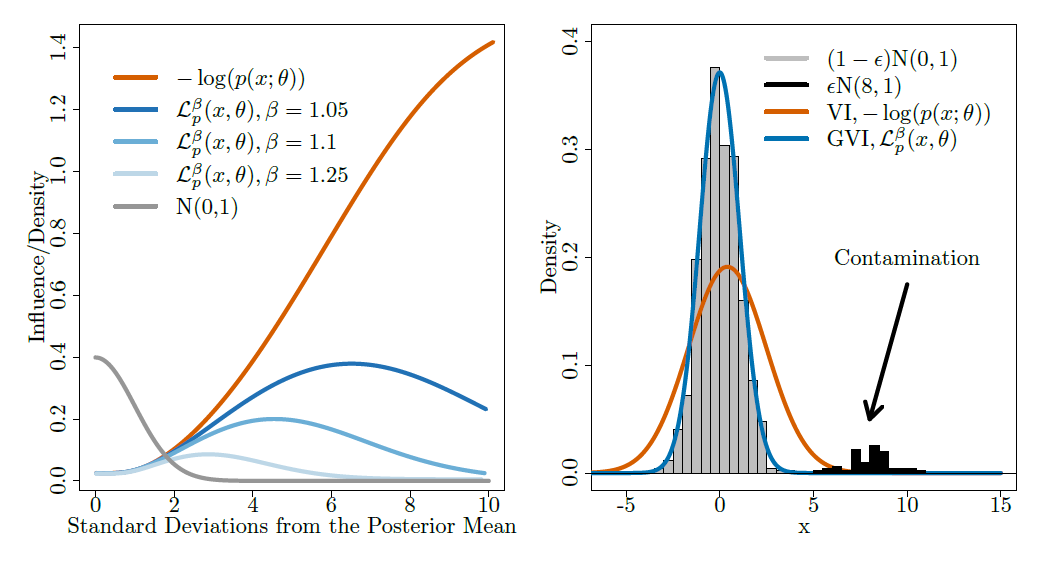
In particolare, la flessibilità nella scelta della loss function rende la GVI robusta e di seguito facciamo vedere il comportamento rispetto agli outliers. La negative log-likelihood risente molto della presenza della contaminazione come si vede dalla funzione d’influenza e dalla posterior risultante.

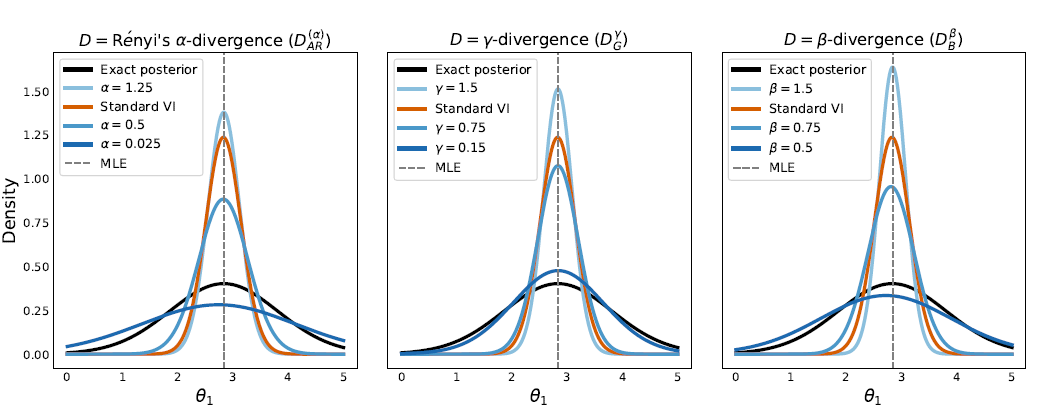
La scelta della divergenza invece influisce sulla robustezza a prior mal specificate e sulla varianza maginale delle posteriori. Come si vede dai grafici, la Kullback-Leibler non è la scelta ottimale in questi casi in quanto tende a sottostimare in maniera evidente la varianza a posteriori, causando errate conclusioni inferenziali.

Algoritmo Black-Box

In quest’ ultimo paragrafo sintetizzo in 3 punti cruciali l’algoritmo di tipo Black-Box (si veda anche Ranganath et al, 2014) che gli autori propongono per la stima:

1. Campiona \(\mathbf{\vartheta}^{(1:S)}\) da \(q(\mathbf{\vartheta}\mid\mathbf{\kappa}_t)\) e calcola le loss function in ogni punto \(\ell_s = \sum_{i=1}^n\ell(\mathbf{\vartheta}^{(s)},x_i)\,\nabla_{\mathbf{\kappa}_t}\log q(\mathbf{\vartheta}^{(s)}\mid\mathbf{\kappa}_t)\);
2. Calcola l’uncertainty quantifier \(\ell_s = \ell_s+\nabla_{\mathbf{\kappa}_t}\mathcal{D}(q\mid\pi)\);
3. Aggiorna i parametri variazionali \(\mathbf{\kappa}_{t+1}=\mathbf{\kappa}_{t}+\rho_t\bar{\ell}\) e il criterio di convergenza. Qui \(\rho_t\) è un learning rate e \(\bar{\ell}\) è la media aritmetica delle \(\ell_s\).

Il gradiente \(\nabla_{\mathbf{\kappa}_t}\mathcal{D}(q\mid\pi)\) è una quantità cruciale in questo algoritmo: può essere calcolato analiticamente per alcune scelte di \(\mathcal{D}\), altrimenti si ricorre ad approssimazioni distorte o non-distorte.

Riferimenti ad altri articoli

1. P. G. Bissiri, C. C. Holmes, S. G. Walker (2016). A general framework for updating belief distributions, Journal of the Royal Statistical Society: Series B.
2. J. Knoblauch, J. Jewson, T. Damoulas (2019). Generalized Variational Inference: Three arguments for deriving new Posteriors.
3. R. Ranganath, S. Gerrish, D. Blei (2014). Black Box Variational Inference, Proceedings of the 17th International Conference on Artificial Intelligence and Statistics.