Laura D'Angelo

PhD student in Statistics @UniPd

Nested mixtures of finite mixtures

5 minute read

Breve introduzione al problema

Dati e obiettivo dell’analisi

L’ambito di riferimento è quello del cosiddetto calcium imaging, una tecnica che permette di osservare l’attività dei neuroni nel tempo tramite l’analisi della concentrazione degli ioni di calcio presente all’interno della cellula. In particolare, in questo esperimento sono osservati i neuroni della corteccia visiva di un topo mentre osserva uno schermo su cui sono presentati stimoli visivi di diverso tipo. L’obiettivo è capire come l’attività dei neuroni vari a seconda dello stimolo visivo a cui il topo è sottoposto.

Per descrivere l’andamento del calcio nel tempo un modello molto usato assume che il livello osservato \(y_t\) sia uguale alla vera concentrazione di calcio (\(c_t\)) più un termine di errore (\(\epsilon_t\)); mentre la vera concentrazione \(c_t\) (latente) è modellata tramite un processo autoregressivo di ordine 1 con degli spike (ovvero dei picchi) in corrispondenza dell’attività neuronale.

\[y_t = c_t + \epsilon_t \qquad \epsilon_t\sim N(0,\sigma^2)\\ c_t = \gamma c_{t-1} + A_t + w_t \qquad w\sim N(0,\tau^2)\]

dove, in corrispondenza di ogni osservazione \(y_t\), è disponibile anche una variabile categoriale \(g_t\in\{1,2,\dots,J\}\) che contiene l’informazione sullo stimolo (“gruppo”) a cui il topo è sottoposto in quell’istante.

I veri parametri di interesse sono gli \(A_t\), \(t=1,2,\dots,T\), che descrivono, per ogni istante temporale, l’attività del neurone. In assenza di attività all’istante \(t\) si avrà \(A_t=0\), mentre in presenza di uno spike il parametro sarà positivo e in tal caso \(A_t\) rappresenta l’ampiezza dello spike.

Poichè l’esperimento è condotto in diverse condizioni sperimentali (stimoli diversi) vogliamo che la risposta del neurone possa variare nei diversi scenari, ma vogliamo comunque utilizzare tutta l’informazione disponibile e quindi non analizzare ogni stimolo separatamente.

Nello specifico, il livello di calcio osservato è definito, condizionatamente all’attività neuronale \(A_t\), come

\[y_t \mid c_{t-1},A_t,\gamma,\sigma^2,\tau^2 \sim N(\gamma c_{t-1} + A_t, \sigma^2 + \tau^2)\]

e l’obiettivo è di definire una distribuzione a priori sugli \(A_t\) in modo da indurre una possibile eterogeneità sulla risposta tra stimoli diversi:

\[(A_t \mid g_t = j) \sim G_j.\]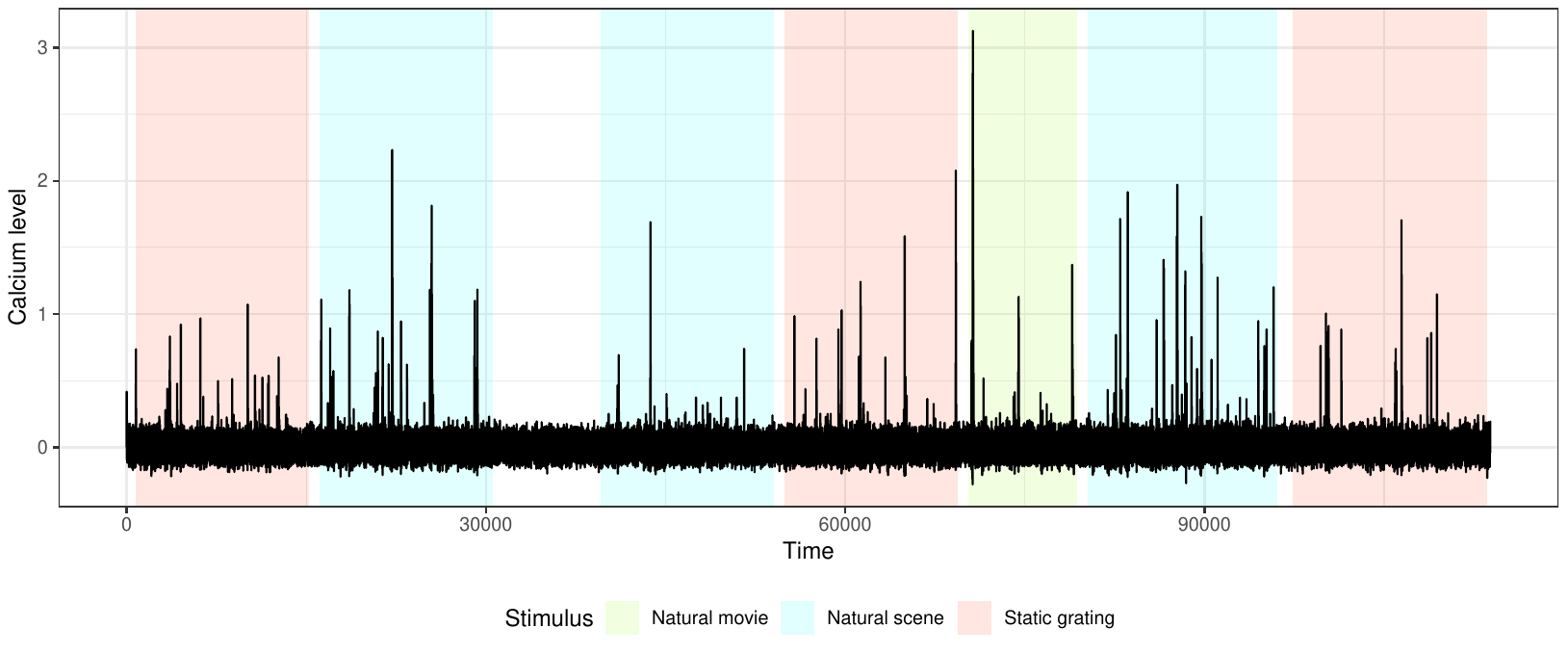

Serie storica di dati di calcium imaging. I colori dello sfondo indicano lo stimolo visivo mostrato in quell'istante.

Modelli “nested”

Nested Dirichlet process

Un approccio Bayesiano nonparametrico per analizzare dati in condizioni di parziale scambiabilità è proposto da Rodríguez, Dunson e Gelfand (2008), ed è il cosiddetto nested Dirichlet process. Questo processo assume che all’interno di ogni gruppo \(g_j\) i parametri siano generati da una comune distribuzione \(G_j\), ovvero

\[(A_t \,\text{ per }\, t \,\text{ tale che }\, g_t=j)\, \sim G_j.\]

Queste distribuzioni \(G_1,\dots,G_J\) sono generate da una distribuzione \(Q\) che è definita come \(Q\equiv DP(\alpha, DP(\beta,G_0))\). Scriverlo in forma di mistura infinita è un po’ più chiaro:

\[G_1,\dots,G_J \mid Q \sim Q \\ Q = \sum_{k=1}^{\infty} \pi_k \delta_{G^*_k} \qquad \{\pi_k\}_{k=1}^{\infty} \sim GEM(\alpha)\\ G_k^* = \sum_{l=1}^{\infty} \omega_{lk} \delta_{A^*_{lk}} \qquad \{\omega_{lk}\}_{l=1}^{\infty}\sim GEM(\beta)\\ A^*_{lk} \sim G_0.\]

Grazie ai due livelli di DP, il processo induce un clustering sia a livello delle osservazioni sia a livello delle distribuzioni tra gruppi diversi. Ovvero, se due gruppi condividono la distribuzione dei parametri, quesi saranno assegnati alla stessa \(G_k^*\). E poichè ogni \(G^*_k\) è anch’essa definita come un DP, anche all’interno di ogni clustering distributivo sarà possibile individuare un clustering delle osservazioni \(y\).

Tuttavia, questa definizione del processo presenta un grosso svantaggio quando applicata in situazioni in cui le distribuzioni tra gruppi non sono troppo diverse: è sufficiente che due distribuzioni \(G^*_k\) e \(G^*_m\) abbiano in comune anche un solo atomo per far sì che vengano fatte collassare insieme e i due gruppi vengano assegnati ad un unico cluster distributivo.

Common Atom Model

Per risolvere questo problema Denti et al. (2020) hanno proposto il cosiddetto common atom model (CAM), che permette di avere distribuzioni distinte anche se parzialmente sovrapposte. La formulazione è molto simile alla precedente, ma la differenza è che gli atomi sono comuni a tutte le distribuzioni, e ciò che permette di ottenere distribuzioni distinte sono solo i pesi \(\omega_{lk}\). Il CAM può essere scritto come

\[G_1,\dots,G_J \mid Q \sim Q \\ Q = \sum_{k=1}^{\infty} \pi_k \delta_{G^*_k} \qquad \{\pi_k\}_{k=1}^{\infty} \sim GEM(\alpha)\\ G_k^* = \sum_{l=1}^{\infty} \omega_{lk} \delta_{A^*_{l}} \qquad \{\omega_{lk}\}_{l=1}^{\infty} \sim GEM(\beta)\\ A^*_{l} \sim G_0.\]

Nested mixtures of finite mixtures

Un noto problema del Dirichlet process è che in alcune circostanze il clustering che produce può non essere soddisfacente e può non riflettere davvero la struttura dei gruppi presenti nei dati. Questo è comune soprattutto quando i gruppi presenti nei dati presentano tutti una numerosità piuttosto equilibrata, e il DP tenderà invece a produrre pochi clusters numerosi e ad inserire piccoli cluster transitori e singoletti. E di conseguenza anche la stima del numero di clusters ne risulterà affetta negativamente.

Per questo motivo di recente è rinato l’interesse verso le misture finite, ma più flessibili rispetto alle misture “standard” in cui il numero di gruppi deve essere fissato in anticipo (e che non richiedano sacrifici alle divinità del RJMCMC per ottenere la posteriori). Una specificazione molto flessibile è stata proposta da Frühwirth-Schnatter, Malsiner-Walli e Grün (2020), che definiscono le cosiddette “generalized mixtures of finite mixtures”. In pratica sono delle misture finite in cui il numero di componenti non è fissato ma è stocastico (e dunque modellato da una priori sui naturali), e in cui si mantiene la distinzione tra componenti e clusters tipica dei modelli nonparametrici. Quindi, analogamente al DP, alcune componenti rimarranno vuote, e il numero di clusters sarà determinato dalle componenti non vuote.

Noi abbiamo deciso di usare queste misture finite al posto delle misture infinite presenti nei due livelli del CAM:

\[G_1,\dots,G_J \mid Q \sim Q \\ Q = \sum_{k=1}^{K} \pi_k \delta_{G^*_k} \\ K \sim p(K), \quad \pi_1,\dots,\pi_K \mid K \sim Dirichlet_K\left(\alpha/K\right); \\ G^*_k = \sum_{l=1}^{L} \omega_{l,k} \delta_{A^*_l}\\ L\sim p(L),\quad \omega_{1,k},\dots,\omega_{L,k} \mid L\sim Dirichlet_L\left(\beta/L\right);\\ A^*_l \sim G_0(A^*_l).\]

e per stimarlo abbiamo riadattato lo slice sampler di Denti et al. (2020) al caso di misture finite, con l’aggiunta degli step descritti da Frühwirth-Schnatter, Malsiner-Walli e Grün (2020) nel loro telescoping sampler per permettere alle dimensioni delle due misture di variare.

Bibliografia

Leave a Comment

Your email address will not be published. Required fields are marked *

Markdown is supported.